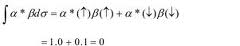SEMUA TENTANG FISIKA
Sabtu, 10 Maret 2012
Selasa, 28 Februari 2012
Model - Model Atom ( Momentum Sudut Orbital Dan Spin )
Fisika Modern MODEL - MODEL ATOM
BAHAN AJAR FISIKA MODERN
Standar Kompetensi : Mahasiswa dapat
memahami fakta, konsep, kaidah, prinsip, prosedur, interaksi, dan mekanisme
partikel dalam fisika modern
Kompetensi Dasar : Mahasiswa
dapat menjelaskan susunan konfigurasi elektron pada atom
Indikator : - Mekanisme elektron dalam atom
- Spektrum dan kedudukan elektron
Materi Pokok : Model – model atom
Submateri Pokok : - Momentum
sudut orbital dan spin - Spektrum
optik
- Prinsip Pauli -
Efek Zeeman
- Susunan berkala
Tujuan
A.
Tujuan PPK
Mahasiswa mampu :
o Menjelaskan orbit dan keberadaan spin elektron
o Menjelaskan dan menerapkan prinsip Paulli
o Menjelaskan peristiwa efek Zeeman
B.
Tujuan Kinerja Ilmiah
o
Membuktikan keberadaan spin elektrom melalui eksperimen
o
Membuktikan kebenaran prinsip Paulli
o
Mengklasifikasi unsur-unsur berdasarkan persamaan sifat-sifatnya
o
Membuktikan
efek Zeeman
C. Tujuan Afektif
o
Mengajukan
pertanyaan dengan baik.
o
Menyampaikan pendapat dengan
baik.
o
Menjadi pendengar yang aktif.
Sumber Pembelajaran : Buku Fisika
Modern karangan Arthur Beiser, Kenneth Krane, Sutrisno, Media Internet, dan
lain – lain
Sarana / Media Pembelajaran : LCD, laptop, slide power point, papan tulis
MODEL – MODEL ATOM
Momentum
Sudut Orbital dan Spin
Elektron dapat terikat pada inti atom melalui gaya tarik
menarik Coulomb. Jika jumlah elektron berbeda dari muatan listrik inti, atom tersebut
dinamakan sebagai ion. Perilaku elektron terikat yang seperti gelombang
dideskripsikan menggunakan fungsi matematika yang disebut orbital atom.
Tiap-tiap orbital atom memiliki satu set bilangan kuantumnya sendiri, yaitu
energi, momentum sudut, dan proyeksi momentum sudut.
Elektron dapat berpindah dari satu orbital ke orbital lainnya
melalui emisi ataupun absorpsi foton yang energinya sesuai dengan perbedaan
potensial antarorbital. Metode perpindahan orbital lainnya meliputi pertumbukan
dengan partikel elektron lain. Agar dapat melepaskan diri dari atom, energi elektron haruslah
ditingkatkan melebihi energi pengikatannya. Ini terjadi pada efek fotolistrik,
di mana foton yang berenergi lebih tinggi dari energi ionisasi atom diserap
oleh elektron.
Oleh karena elektron bermuatan, ia menghasilkan momen
magnetik orbital yang proposional terhadap momentum sudut. Keseluruhan momen
magnetik sebuah atom adalah setera dengan jumlah vektor momen magnetik orbital
dan momen magnetik spin keseluruhan elektron dan inti atom. Namun, momen
magnetik inti sangatlah kecil dan dapat diabaikan jika dibandingkan dengan
elektron. Momen magnetik dari dua elektron yang menduduki orbital yang sama
(disebut elektron berpasangan) akan saling meniadakan.
Ikatan kimia antaratom terjadi sebagai akibat dari
interaksi elektromagnetik. Ikatan yang terkuat terbentuk melalui perkongsian elektron maupun
transfer elektron di antara atom-atom, mengizinkan terbentuknya molekul. Dalam
molekul, pegerakan elektron dipengaruhi oleh beberapa inti atom dan elektron
menduduki orbital molekul, sama halnya dengan elektron yang menduduki orbital
atom pada atom bebas. Faktor mendasar pada struktur molekul adalah keberadaan pasangan
elektron. Kedua elektron yang berpasangan memiliki spin yang berlawanan,
mengizinkan keduanya menduduki orbital molekul yang sama.
Degenerasi
sebanyak n2 dari tingkat energi atom hidrogen disebabkan oleh adanya nilai l yang berbeda untuk suatu n tertentu. Namun dengan adanya suatu interaksi lain/bukan interaksi Coulomb
mengakibatkan terpecahnya tingkat energi untuk suatu bilangan kuantum n. Terjadinya pemecahan tingkat energi ini mengakibatkan garis spectrum yang dipancarkan
menjadi lebih banyak dan disebut spectrum struktur halus.
Ada beberapa garis spektrum halus yang tidak dapat
dijelaskan karena adanya multiple l Misalnya yang terjadi pada garis kuning dari natrium sebagai hasil
transisi dari n = 3, l = 1(3p) ke n = 3, l
= 0 (3s). Goudsmit dan Uhlenbeck 1925 mengusulkan bahwa elektron memiliki suatu
komponen sudut intrinsik yang tidak dipengaruhi oleh gerak orbitalnya dan disebut sebagai
spin elektron. Hal ini dapat menggambarkan bahwa elektron berotasi pada sumbunya sehingga
menghasilkan momentum sudut spin S.
Karena elektron bermuatan listrik negatif, maka gerak rotasinya
menghasilkan medan magnet dengan momen magnetnya µ, berlawanan arah Ls.
Elektron yang berspin tersebut di dalam atom mengedari
inti, namun dilihat oleh elektron (jika pengamat diam terhadap elektron), inti yang bermuatan
positif tersebut mengedari elektron sehingga dari sisi elektron terdapat medan
magnet akibat edaran inti tersebut.
Suatu keadaan dengan nomor kuantum momentum sudut spin S
(lebih sering diangkat sebagai bilangan kuantum spin) karena pengaruh medan
magnet ini terkuantisasi ruang sebanyak 2s + 1. Dari pengamatan, nilai tersebut
selalu sama dengan 2 sehingga 2s + 2 Atau s = ½
Besar momentum sudut spin :
...(1)
Sedangkan komponen
momentum sudut spin ke arah medan magnet adalah :
Sz = msh ... (2)
Dengan ms
adalah bilangan kuantum magnetik spin yang dapat bernilai -s dan +s atau -½ atau
½.
Orbital elektron dan tingkat
energi dari sistem elektron banyak diklasifikasikan menjadi 1s, 2s,
2p, 3s, 3p, 3d, dan seterusnya dalam kasus atom-atom hidrogenik. Masalahnya
adalah bagaimana elektron-elektron tersebut didistribusikan ke dalam orbital
elektron. Apakah seluruh elektron digabungkan ke dalam orbital yang paling
stabil yaitu orbital 1s dengan energi
terendahnya? Kesimpulan dari teori kuantum adalah bahwa hanya ada dua elektron
yang dapat menempati orbital yang sama. Aturan ini berkaitan dengan momentum
sudut khusus yang disebut sebagai spin elektron.
Keberadaan spin
elektron dibuktikan melalui beberapa eksperimen yaitu :
1.
Eksperimen
berkas atom oleh Stern dan Gerlach
Aliran
atom dapat dihasilkan dalam sebuah ruang vakum melalui nozel setelah melakukan
evaporasi perak atau logam alkali dengan pemanasan. Aliran atom yang demikian
itu dalam vakum disebut sebagai berkas atom. O. Stern dan W. Gerlach menemukan
pada tahun 1922 bahwa berkas atom perak atau atom natrium, yang memiliki hanya
satu elektron pada kulit terluar, berpisah membentuk dua garis dalam sebuah
medan magnet tidak homogen.
Di dalam eksperimen ini berkas atom perak
yang netral dilewatkan dalam suatu medan magnet tak homogen dalam arah sumbu z
(Gb. 1). Jika
atom tersebut mempunyai momen magnet µ, maka energi interaksinya dengan
medan magnet adalah : E = -µβ ... (3)
Di dalam medan magnet dengan gradien dβ/dz, maka atom tersebut
mengalami gaya arah z sebesar : Fz
= µz dβ/dz ...
(4)
Secara klasik, momen dipol magnet terorientasi secara acak
sehingga diharapkan berkas atom setelah melewati medan magnet menjadi melebar.
Hasil dalam eksperimen tersebut menunjukkan bahwa berkas atom terpecah menjadi
dua komponen diskret yang berarti bahwa hanya ada dua kemungkinan nilai dari µz, karena atom perak hanya mempunyai sebuah elektron di kulit
terluarnya, hasil eksperimen di atas menunjukkan bahwa spin elektron juga hanya
mempunyai dua kemungkinan nilai.
Eksperimen ini memberikan gambaran bahwa sebuah
elektron memiliki sebuah momen magnetik, yang merupakan sifat magnetik yang
berkaitan dengan arus listrik melingkar.
Gambar 1. Eksperimen berkas atom oleh Stern dan
Gerlach.
1.
Garis
ganda (doblet) dalam spektrum atom logam alkali
Sebuah
warna oranye dari reaksi pembakaran natrium dapat dipancarkan dari lampu
lecutan listrik dengan uap natrium. Garis-garis hitam (garis Fraunhofer)
ditemukan dalam spektrum dari matahari terdiri dari garis-garis dengan panjang
gelombang yang sama sebagaimana spektrum natrium dan disebut sebagai
garis-garis D. Garis-garis D dari natrium berasal dari transisi antara tingkat
3s dan 3p dan pada garis-garis itu diamati terdiri dari dua garis yang
berdekatan (doblet) pada panjang gelombang 5895.93 Å dan 5889.97 Å. Doblet
seperti itu juga ditemukan pada atom alkali yang lain dan jarak pemisahannya
diketahui akan semakin membesar dengan susunan Li < Na < K < Rb <
Cs. S.A. Goudsmit dan G.E. Uhlenbeck mengusulkan bahwa pemisahan garis spektra
disebabkan oleh momen magnetik dari sebuah elektron yang berkaitan dengan
gerakan melingkarnya. Karena momentum sudut dikaitkan dengan gerakan melingkar
dari sebuah muatan listrik, momentum sudut ini yang menjadi asal usul momen
magnetik dari sebuah elektron. Momentum sudut yang berkaitan dengan gerakan
melingkar oleh sebuah elektron disebut sebagai spin elektron.
Dalam usaha untuk
membahas spin elektron dalam mekanika kuantum, operator harus diperkenalkan
seperti pada momentum sudut orbital. Marilah kita menuliskan momen sudut spin
sebagai s topi dan dengan komponen-z ditulis sebagai sz. Dengan mengambil analogi terhadap momentum sudut orbital, fungsi eigen
yang umum Γ untuk s topi dan sz diharapkan ada dan harus memiliki hubungan sebagai berikut :
Dengan eksperimen,
berkas atom dipisahkan menjadi dua komponen dalam sebuah medan magnet dan
spektra logam alkali terpisahkan menjadi 2 garis. Berdasarkan penemuan ini, ms disimpulkan hanya memiliki
2 nilai yang mungkin. Ini mengikuti ketentuan bahwa 2s + 1 = 2 dan karenanya kita mendapatkan s, s = 1/2, ms
= ±1/2. Harus dicatat bahwa bilangan kuantum spin adalah sebuah setengah bilangan
bulat dengan hanya satu nilai yaitu s = 1/2. Nilai yang dibolehkan
untuk ms dibatasi hanya pada nilai ±1/2. Spin adalah
momentum sudut yang sangat khusus jika dibandingkan dengan momentum sudut
orbital.
Meskipun sifat
yang khusus dari momentum sudut spin sangat sulit untuk dimengerti secara
konseptual, perhitungan dan perlakuan matematikanya sangatlah sederhana. Karena
hanya ada dua keadaan, maka hanya terdapat dua buah fungsi eigen. Biasanya
fungsi spin berkaitan dengan dengan ms = 1/2 dinyatakan sebagai
α, dan fungsi spin yang lain untuk ms
= -1/2 dinyatakan sebagai β.
Dalam kaitan
dengan orientasi dari momen magentik yang berkaitan dengan gerakan berputar,
arah ke atas disebut sebagai spin α dan arah ke
bawah disebut sebagai spin β. Variabel σ untuk fungsi spin α(σ),
β(σ) disebut sebagai koordinat spin. Meskipun
keberartian dari koordinat spin σ tidak jelas, kita tidak perlu untuk memperhatikan
apa yang direpresentasikannya.
Koordinat spin
adalah koordinat ke empat yang mengkuti tiga koordinat untuk posisi dalam ruang
tiga dimensi. Secara formal, nilai yang dimungkinkan untuk koordinat spin hanya
ada dua kasus yaitu orientasi keatas σ = ↑ dan orientasi ke bawah σ = ↓.
Probabilitas untuk
menemukan sebuah elektron pada σ = ↑ adalah
sama dengan 1 dalam keadaan spin ke atas α dan 0 dalam keadaan spin ke bawah β. Di sisi yang lain, probabilitas untuk menemukan sebuah elektron pada
keadaan σ = ↓ adalah sama dengan 0 dalam keadaan
spin ke atas α dan 1 dalam keadaan spin ke bawah β.
Dalam mekanika
kuantum, beberapa integral perlu dihitung dalam kaitannya dengan probabilitas
dan normalisasi. Sebagaimana untuk spin, sebuah penjumlahan yang sederhana untuk
dua koordinat saja, ↑ dan ↓ yang diperlukan. Sebagai contoh persamaan (9) akan menghasilkan :
...(10)
Dan hal yang sama
...(11)
Sebagai tambahan
...(12)
Sebagaimana dapat
dilihat dari perhitungan-perhitungan ini, fungsi-fungsi spin α,
β dalam persamaan (9) memenuhi sifat ortonormalitas.
Untuk sebuah
fungsi ψ dari sebuah elektron dengan memperhatikan
spin elektron, terdiri dari variabel untuk koordinat spasial x, y, z dan koordinat spin σ. Jika komponen dari spin elektron sz
memiliki suatu nilai – nilai yang pasti, fungsi spin dapat terdiri dari α atau β. Ini akan memberikan keadaan bahwa fungsi orbital
spasial untuk koordinat kartesian φ(x,y,z) menghasilkan pasangan fungsi gelombang berikut untuk elektron-elektron
yang di akomodasi dalam orbital spasial ini.
Persamaan-persamaan
ini berkaitan dengan sebuah aturan bahwa jumlah elektron dalam setiap orbital
spasial (dalam kasus sebuah atom dengan orbital 1s, 2s, 2px, 2py,
3dxy, dll.) haruslah tidak melebihi dua.
Prinsip Pauli
Pertanyaan tentang
berapa banyak elektron yang dapat menempati sebuah orbital atomik seperti pada
orbital 1s adalah masalah yang sangat
penting dalam hubungannya dengan spektra atomik dan sifat-sifat atomiknya.
Solusi dari masalah ini diberikan oleh Pauli pada tahun 1924 dan aturan ini
disebut sebagai prinsip Pauli atau prinsip eksklusi Pauli.
Prinsip Pauli yaitu tidak
mungkin di dalam atom terdapat 2 elektron dengan keempat bilangan kuantum yang
sama. Hal ini berarti, bila ada dua elektron yang mempunyai bilangan kuantum
utama, azimuth dan magnetik yang sama, maka bilangan kuantum spinnya harus
berlawanan.
Setiap orbital
dapat ditempati oleh sebuah elektron dengan spin α atau spin β, akan tetapi ia tidak dapat ditempati
oleh dua atau lebih elektron dengan spin yang sama. Aturan ini ditetapkan oleh
Pauli berdasarkan hasil eksperimen seperti pada spektra atomik. Hal yang sangat
penting adalah bahwa setiap elektron memenuhi aturan ini, dalam hubungannya
dengan pembentukan fungsi gelombang elektron banyak.
Marilah kita
meninjau dua elektron. Satu terletak pada sebuah koordinat q1 dan yang lain pada q2. Keadaan ini dinyatakan dengan sebuah fungsi
gelombang yang ditulis sebagai Ψ(q1,q2). Hal yang sama sebuah keadaan untuk dua
elektron dengan koordinat yang saling bertukar dapat ditulis sebagai Ψ(q1,q2). Meskipun Ψ(q1,q2) dan Ψ(q2,q1) secara matematika berbeda ekspresi yang
menyatakan penomoran elektron-elektron sebagai 1 dan 2, kita tidak dapat mengenal
setiap perbedaan dalam penomoran ketika kita mengamati elektron. Ini akan
mengakibatkan bahwa probabilitas untuk menemukan elektron nomor 1 pada q1 dan elektron nomor 2 pada q2 harus sama dengan
probabilitas untuk menemukan elektron nomor 1 pada q2 dan elektron nomor 2 pada q1. Kondisi ini dinyatakan dengan persamaan berikut :
Dengan mencatat
bahwa fungsi gelombang secara umum adalah bilangan kompleks, kita akan
memperoleh :
Pilihan awal dari
dua elektron dan juga geometrinya dapat diambil sembarang. Dengan demikian
adalah tidak masuk akal untuk mengasumsikan bahwa konstanta θ dalam persamaan (16) berbeda dan bergantung
pada pilihan dari elektron dan geometrinya. Karenanya hubungan yang sama harus
dipenuhi untuk sebuah pertukaran dari q1
dan q2.
Dua persamaan ini akan menghasilkan :
Sehingga,
Dan akan menghasilkan :
Dan kemudian
Kita bisa
menyatakan bahwa tanda dari sebuah fungsi gelombang dapat berubah atau tidak,
ketika sebuah pasangan partikel yang identik dipertukarkan koordinat
geometriknya. Sifat dari partikel akan menentukan yang mana dari dua
kemungkinan tersebut yang dapat terjadi.
1.
Untuk
tanda yang tidak berubah dengan sebuah perkalian +1, fungsi gelombangnya
simetrik terhadap pertukaran koordinat dan partikel tipe ini disebut sebagai
partikel Bose atau boson
2.
Untuk
tanda yang berubah dengan sebuah perkalian -1, fungsi gelombangnya antisimetrik
terhadap pertukaran koordinat dan partikel tipe ini disebut sebagai partikel
Fermi atau fermion.
Prinsip Pauli
menunjukkan bahwa elektron adalah fermion dan fungsi gelombang akan berubah
tandanya jika terjadi pertukaran koordinat. Jika sebuah fungsi gelombang
simetrik diijinkan untuk elektron-elektron, ini akan berlawanan dengan prinsip
Pauli. Sebagai contoh, marilah kita mengasumsikan bahwa terdapat dua elektron
menempati orbital 1s dengan spin α. Fungsi gelombang Ψ yang berkaitan dengan asumsi ini dinyatakan dengan fungsi orbital φ1s sebagai berikut :
 ... (22)
... (22)
Sekarang, marilah
kita menukarkan koordinat dari nomor 1 dan nomor 2 dan kemudian kita
mendapatkan :
 ... (23)
... (23)
Ini secara jelas
menunjukkan simetri fungsi gelombang untuk boson. Dengan kata yang lain, jika
elektron-elektron tersebut adalah foston, akan ada dua atau lebih elektron yang
menempati keadaan 1s yang sama dalam
atom. Akan tetapi, keadaan ini akan berlawanan dengan prinsip Pauli.
Di sisi lain,
untuk fungsi gelombang yang simetrik, tidak ada keadaan yang berlawanan dengan
prinsip Pauli yang dapat diterima. Gambaran ini dapat dengan mudah dilihat ketika
sebuah fungsi gelombang determinan, yang diusulkan oleh J. C. Slater dan
disebut sebagai determinan Slater, digunakan.
Marilah kita
memperkenalkan fungsi orbital ψ1 dan ψ2 yang juga terkandung koordinat spin sebagai
tambahan dari koordinat spasial. Kita menulis fungsi gelombang Ψ untuk sistem dengan 2 elektron sebagai determinan
berikut :
... (24)
Setelah melakukan
ekspansi, kita akan mendapatkan persamaan berikut yang menunjukkan karakter
antisimetrik.
 ... (25)
... (25)
Harus dicatat di
sini bahwa Hamiltonian invarian terhadap pertukaran koordinat dari partikel
identik dan bahwa jika Ψ = ψ1(q1)ψ2(q1) adalah sebuah solusi dari ψ = Eψ, maka ψ = ψ1(q2)ψ2(q2) juga merupakan solusi dari ψ = Eψ. Ini akan diikuti dengan keadaan bahwa determinan
di atas memenuhi hubungan Ψ = EΨ. Dengan menggunakan determinan yang diusulkan
oleh Slater, kita dapat membangun sebuah fungsi gelombang antisimetrik yang
terdiri dari fungsi-fungsi orbital.
Sekarang kita
mengasumsikan lagi bahwa ada dua elektron yang menempati orbital 1s dengan spin yang sama yaitu spin α. Dalam kasus ini, ψ1 = φ1s .α,
ψ2 = φ1s .α, atau ψ1s = ψ2. Dengan demikian, kita dapat mengabaikan
indeks dengan ψ1 = ψ2 = ψ. Fungsi gelombang determinan untuk sistem
ini akan menjadi :
... (26)
Nilai yang sama
dengan nol pada determinan ini adalah hasil yang pasti berkaitan dengan aturan
umum dari determinan bahwa sebuah determinan dengan
sebuah pasangan pada baris yang sama atau kolom yang sama akan sama dengan nol.
Jika aturan ini digunakan, determinan dalam persamaan (26) dengan mudah akan
diketahui sama dengan nol tanpa perlu dilakukan ekspansi.
Berdasarkan pada hasil ini, dengan mudah
terlihat bahwa sebuah konfigurasi elektron yang menempati orbital dan melanggar
prinsip Pauli akan menghasilkan fungsi gelombang yang secara fisik tidak dapat
dimungkinkan dengan sebuah nilai yang sama dengan nol atau mengindikasikan
ketidakberadaan partikel. Perhatian yang lebih detail dan hati-hati telah
menunjukkan bahwa fungsi gelombang yang antisimetrik, kompatibel dengan prinsip
Pauli. Ini akan memberikan
pemahaman bahwa elektron adalah fermion dengan karakter antisimetrik.
Karenanya, lebih
mudah untuk menyatakan sebuah fungsi gelombang atom banyak sebagai sebuah
determinan dari sebuah matrik dengan di dalamnya tersusun fungsi orbital.
Sebuah fungsi gelombang determinan dibentuk dari fungsi orbital ternormalisasi
sebagai sebuah fungsi untuk elektron banyak, dengan menyatakan bahwa sebuah
faktor 1/N! ada di dalamnya.
Dalam usaha untuk
menyatakan sebuah fungsi gelombang determinan dalam bentuk yang singkat, kita
dapat menuliskannya sebagai |ψ1ψ2…ψN| melalui sebuah barisan fungsi orbital {ψ1i} di antara sebuah pasangan garis vertikal. Sebuah
susunan dari fungsi orbital dalam sebuah bentuk matriks adalah ekivalen dengan
membuat sebuah konfigurasi elektron yang berkaitan dengan keberadaan elektron
pada masing-masing orbital.
Dengan kata lain, hal ini mengakibatkan
bahwa elektron akan menempati tingkat energi masing-masing. Sehingga, keadaan di mana elektron menempati orbital atau tingkat tertentu disebut
sebagai konfigurasi elektron atau konfigurasi elektronik. Fungsi gelombang
determinan digunakan sebagai perumusan matematik dari konfigurasi elektron.
Metoda konseptual untuk membuat konfigurasi elektron dapat dipahami sebagai
pengisian orbital oleh elektron.
Pembentukan fungsi
gelombang determinan tidak memiliki kelebihan fisik yang penting jika nilainya
sama dengan nol berlawanan dengan keberadaan elektron-elektron. Untuk dapat
menghindari situasi yang tidak wajar, kehati-hatian harus dilakukan sedemikian
rupa sehingga tidak ada fungsi orbital yang identik yang berada dalam barisan
orbital dalam determinan atau dengan kata lain, kita tidak menggunakan
kombinasi yang sama dari sebuah fungsi koordinat spasial dan sebuah fungsi spin
lebih dari sekali dalam determinan.
Penggunaan fungsi
gelombang determinan menjamin dipenuhinya sifat antisimetrik elektron, dan
karenanya konfigurasi elektron yang tidak sejalan dengan prinsip Pauli secara
otomatis dapat dihindari karena nilai dari determinan yang demikian itu sama
dengan nol.
Susunan Berkala
Susunan berkala disebut juga
sebagai sistem periodik unsur-unsur. Seperti kita ketahui, telah dikenal lebih
dari 100 unsur terdapat di alam dan masing-masing unsur memiliki sifat-sifat
yang berbeda. Oleh karena itu untuk mempelajari kelakukan setiap unsur, perlu
diadakan klasifikasi unsur-unsur dalam golongan-golongan yang didasarkan atas
persamaan sifat-sifatnya. Unsur-unsur yang memiliki sifat-sifat yang mirip
dimasukan kedalam satu golongan, sehingga dapat dipelajari dengan lebih mudah
dan lebih sistematis, sekaligus dapat melihat hubungan antara satu hal dengan
hal lainnya.
Secara singkat, guna susunan
berkala adalah untuk meramalkan dan mengetahui sifat unsur, sehingga kita dapat
meramalkan dan mengetahui berbagai gejala / kejadian di alam. Contohnya :
1.
Bagi
orang geologi, dapat diramalkan bahwa rubidium mungkin terdapat sebagai trace
elemen dari mineral potasium
2.
Bagi
orang kimia, dapat menjelaskan kenapa Na dapat berikatan dengan Cl, dan hanya
atom Cl yang dapat terikat
3.
Bagi
orang mesin, dapat menjelaskan kenapa logam pada umumnya mudah menghantarkan
panas, bersifat magnet.
Telah dikatakan bahwa susunan
berkala yang sekarang digunakan merupakan fungsi berkala dari nomor atom. Nomor
atom tersebut menunjukan jumlah proton atau jumlah elektron, maka susunan
berkala ini disusun berdasarkan konfigurasi elektron dari atom unsur-unsur.
Unsur-unsur dengan konfigurasi elektron yang mirip, mempunyai sifat kimia dan
sifat fisika yang mirip. Berarti konfigurasi elektron berhubungan dengan sifat
unsur.
Susunan berkala terdiri dari ::
a.
Baris
mendatar dengan nomor atom yang berurut disebut perioda. Ada tujuh perioda,
yaitu Perioda (I) sampai dengan (VII)
b.
Baris
vertikal disebut grup atau golongan.
.jpeg)
Gambar 2. Susunan Berkala Gambar 3. Tabel Periodik

Gambar 4. Muatan elektron Gambar 5. Elemen – elemen pada Tabel
Periodik
Spektrum Optik
Spektrum optik merupakan bagian dari spektrum elektromagnetik yang tampak oleh mata manusia.
Radiasi elektromagnetik dalam rentang panjang gelombang ini disebut sebagai cahaya
tampak atau cahaya saja. Spektrum optik adalah spektrum yang
kontinu sehingga tidak ada batasan yang tepat dari spektrum optic antara satu warna dengan warna lainnya.
Mata normal manusia
dapat menerima panjang gelombang dari 400 sampai 700 nanometer (nm), meskipun
beberapa orang dapat menerima panjang gelombang dari 380 sampai 780 nm. Mata
yang telah beradaptasi dengan cahaya biasanya memiliki sensitivitas maksimum di
sekitar 555 nm, di wilayah hijau dari spektrum optik. Warna pencampuran seperti
pink atau ungu, tidak terdapat dalam spektrum ini karena warna-warna tersebut hanya akan didapatkan
dengan mencampurkan beberapa panjang gelombang.
Gambar 6. Warna – warna spektrum
Panjang gelombang yang
kasat mata diartikan oleh jangkauan spektral jendela optik, wilayah spektrum
elektromagnetik yang melewati atmosfer. Radiasi elektromagnetik di luar
jangkauan panjang gelombang optik, atau jendela transmisi lainnya hampir
seluruhnya diserap oleh atmosfer. Dikatakan jendela optik karena manusia tidak
bisa menjangkau wilayah di luar spektrum optik. Inframerah terletak sedikit di
luar jendela optik, namun tidak dapat dilihat oleh mata manusia.
Banyak spesies yang
dapat melihat panjang gelombang di luar jendela optik. Lebah dan serangga
lainnya dapat melihat cahaya ultraviolet, yang membantu mereka mencari nektar
di bunga. Spesies tanaman bergantung pada penyerbukan yang dilakukan oleh
serangga sehingga yang berkontribusi besar pada keberhasilan reproduksi mereka
adalah keberadaan cahaya ultraviolet, bukan warna yang bunga perlihatkan kepada
manusia. Burung juga dapat melihat ultraviolet (300-400 nm).
Berikut batasan untuk
warna-warna spektrum:
·
Ungu 380-450
nm
·
Biru 450-495 nm
·
Hijau 495-570 nm
·
Kuning 570-590 nm
·
Jingga 590-620 nm
·
Merah 620-750 nm
Efek Zeeman
Efek
Zeeman adalah pemisahan
sebuah garis spektrum menjadi beberapa komponen disebabkan oleh adanya medan magnet. Periswa efek Zeemen terjadi ketika
sebuah atom dipengaruhi oleh medan magnet maka spektrumnya akan terpecah dan
energi yang dihasilkan akan berkurang.
Tahun 1896 Zeeman
mengulangi eksperimen Faraday dengan peralatan yang lebih sensitif, sehingga
menemukan bahwa Faraday memang betul. Dengan menggunakan alat modern dan di dalam
medan magnetik yang sangat kuat ditemukan setiap garis spektrum terpisah
menjadi beberapa komponen bila medan magnetik tersebut dihidupkan.
Spektrum garis atomik teramati
saat arus listrik dialirkan melalui gas di dalam sebuah tabung lecutan gas.
Garis-garis tambahan dalam spektrum emisi teramati jika atom-atom tereksitasi
diletakkan di dalam medan magnet luar. Satu garis di dalam spektrum garis emisi
terlihat sebagai tiga garis (dengan dua garis tambahan) di dalam spektrum
apabila atom diletakkan di dalam medan magnet. Terpecahnya satu garis menjadi
beberapa garis di dalam medan magnet dikenal sebagai efek Zeeman.
Gambar 7. Pemisahan garis spektrum
atomik di dalam medan magnet
Efek Zeeman tidak dapat
dijelaskan menggunakan model atom Bohr. Dengan demikian, diperlukan model atom
yang lebih lengkap dan lebih umum yang dapat menjelaskan efek Zeeman dan
spektrum atom berelektron banyak.
Gambar
8. Efek Zeeman mengenai transisi energi elektron
dalam atom
yang berada dalam suatu medan magnet
B
Peristiwa efek Zeeman merupakan bukti yang jelas
dari kuantisasi ruang. Dikarenakan m1 dapat memiliki 2l + 1 harga dari +l melewati 0 hingga
–l, suatu keadaan dimana bilangan kuantum orbital l terpecah menjadi 2l +
1. Jika atom m buah pecahan sub keadaan yang berbeda energi tersebut diletakkan dalam medan magnetik.
Namun, karena perubahan m1 = 0, ± 1, kita dapat mengharapkan bahwa garis spektral D terbatas pada yang timbul dari transisi
antara dua keadaan dengan satu berbeda hanya terpecah menjadi tiga
komponen, seperti terlihat pada gambar (8). Efek Zeeman normal
terdiri dari garis spektral berfrekuensi vo
terpecah menjadi tiga komponen berfrekuensi. Dalam menganalisis transisi antara
keadaan ml yang berbeda, seringkali kita perlu untuk menggunakan aturan seleksi
kedua : bahwa transisi yang terjadi hanyalah yang mengubah ml sebanyak 0, +1,
atau -1. Perubahan ml
sebanyak dua atau lebih tidak diperkenankan.
Gerak magnetik elektron
orbital dalam sebuah atom hidrogen bergantung dari momentum sudut l, besar, serta arah l terhadap medan akan menentukan berapa
besar sumbangan magnetik pada energi total atom apabila terletak dalam medan
magnetik. Momen magnetik adalah sebuah arus (current
loop) dimana :  ...
(27)
...
(27)
Dalam peristiwa efek Zeeman
ini, apabila seberkas atom hidrogen yang terdiri atas jumlah bagian atom yang
sama (masing-masing dalam keadaan ml = -1, 0, dan +1) dilewatkan
pada suatu daerah yang didalamnya terdapat suatu medan magnet tak seragam.
Gambar
8. Garis spektral yang timbul dari transisi
Karena atom-atom dengan ml
= +1 mengalami neto gaya ke atas, maka mereka dibelokkan ke atas, atom-atom
dengan ml = -1 dibelokkan ke bawah, dan atom dengan ml =
0 tidak dibelokkan. Setelah melewati medan magnet, berkas atom dijatuhkan pada
suatu layar, di situ berkas membentuk sebuah titik terang. Apabila medan magnetnya dihilangkan, maka
hanya terdapat satu titik di pusat layar, karena berkas sama sekali tidak
mengalami pembelokan. Apabila medan magnetnya dinyalakan, maka akan terdapat
tiga buah titik pada layar, yaitu
satu di pusat (berkaitan
dengan ml = 0), satu di atas pusat (ml
= +1), dan satu di bawah pusat (ml
= -1).
Kesimpulan
Elektron dapat terikat pada inti atom melalui gaya tarik
menarik Coulomb. Elektron dapat berpindah dari satu orbital ke orbital lainnya
melalui emisi ataupun absorpsi foton yang energinya sesuai dengan perbedaan
potensial antarorbital. Metode perpindahan orbital lainnya meliputi pertumbukan
dengan partikel elektron lain.
Prinsip
Pauli yaitu tidak mungkin di
dalam atom terdapat 2 elektron dengan keempat bilangan kuantum yang sama. Hal
ini berarti, bila ada dua elektron yang mempunyai bilangan kuantum utama,
azimuth dan magnetik yang sama, maka bilangan kuantum spinnya harus berlawanan.
Susunan berkala atau sistem periodik unsur-unsur
adalah susunan lebih dari 100 unsur dengan sifat yang berbeda dan unsur-unsur yang memiliki sifat-sifat yang
mirip dimasukan kedalam satu golongan, sehingga dapat dipelajari dengan lebih
mudah dan lebih sistematis, sekaligus dapat melihat hubungan antara satu hal
dengan hal lainnya.
Spektrum optik adalah spektrum yang
kontinu sehingga tidak ada batasan yang tepat dari spektrum optik antara satu warna dengan warna lainnya. Berikut batasan untuk
warna-warna spektrum:
·
Ungu 380-450
nm
·
Biru 450-495 nm
·
Hijau 495-570 nm
·
Kuning 570-590 nm
·
Jingga 590-620 nm
·
Merah 620-750 nm
Efek
Zeeman adalah pemisahan
sebuah garis spektrum menjadi beberapa komponen disebabkan oleh adanya medan magnet. Periswa efek Zeemen terjadi ketika
sebuah atom dipengaruhi oleh medan magnet maka spektrumnya akan terpecah dan
energi yang dihasilkan akan berkurang.
Pertanyaan
- Bagaimana proses perpindahan elektron dgn proses emisi ?
- Mengapa hanya ada 2 nilai spin (1/2 dan -1/2) ?
Langganan:
Postingan (Atom)